Part three covered the concept of emulating tube amplifiers with a computer.

Time to put it all together. You now know that playing an electric guitar through a tube amplifier typically distorts the signal in a desirable fashion. You know that emulating a tube amplifier is great for keeping on good terms with your neighbours. And you know that laptops offer a convenient way to do that.

The problem boils down to finding algorithms which a laptop can use to reproduce the transformation a guitar signal undergoes as it passes through an amplifier. Two such algorithms were discussed in part three. Now it's time to look at what was done in building Swanky Amp.

Circuit simulation

A good place to start is with a schematic of a tube amplifier, which is effectively as detailed a mathematical description of that amplifier as you can get. In the case of Swanky Amp, a schematic closely resembling that of a Tweed Deluxe was used as a starting point. Clever people have written software which simulates the evolution of a signal in any part of such a schematic. In this way, the transformation of the guitar signal can be reproduced as accurately as the schematic (plus description of the tubes) allows. And those descriptions are quite accurate.

The following image shows the simulated outcome of an overdriven sinusoidal signal transformed by the first tube in the amp. The most visible effect is the clipping at the top of the waveform, but there's clearly a lot more going on. The waveform is inverted, it is shifting upward over time, the clip corners are rounded … The resulting distortion is quite different from that obtained with the hard clipping shown in part three. And the distortion will change over time as the level and shape of the clip changes.

A faster approach

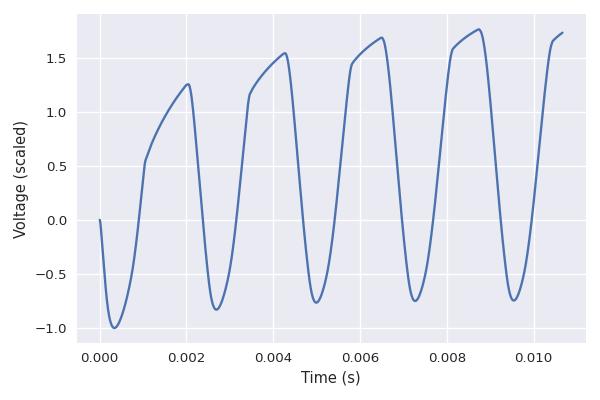
It might then seem that the problem is solved: just pipe the guitar signal into the simulation! Except that while 2 billion transistors seems like a large number (and it is), the calculations required to simulate the circuit are so numerous that it takes a modern laptop a few seconds to simulate a few milliseconds of signal. This is highly problematic since the computer needs to be able process the signal at least as fast as you’re playing your guitar. And in fact, it should be much faster since your laptop also needs some spare transistors to keep doing normal laptop things (like streaming cat videos).

Attempt number two: the problem boils down to finding an algorithm which transforms a signal in a manner roughly equivalent to a tube amplifier, and which can be computed quickly. The approaches described in part three lean more towards the "roughly" rather than the "equivalent" side of things.

Will Pirkle's Designing Audio Effect Plug-Ins in C++ does a fantastic job of this. In his approach, the circuitry is broken down into groups of circuit elements, and C++ algorithms are written to emulate the transformation of the signal as it passes through each group. Then, by running the guitar signal through successive such algorithms, the overall amplifier transformation can be emulated.

An example of a group useful for analyzing how a triode transforms a signal.

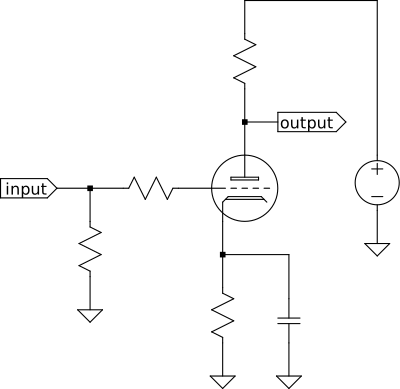
A similar breakdown can be seen here. By analyzing the circuit around a tube and cross-referencing with manufacturer information, it's possible to mathematically describe how that portion of circuit is expected to transform the signal. Translating that mathematical description into a C++ algorithm is then fairly straightforward.

Recovering the detail

While this approach can lead to satisfactory results, some of the dynamic behaviours of tube amps are ignored. This is due to the fact that the groups are treated as independent of one-another. Whereas in reality, they are all contected in the same circuit and share some degree of coupling. This coupling is easily captured in the simulation, but is hard to work into the mathematical description of the individual groups.

For example, the following two images show a pulse signal, and the resulting change of voltage on the plate of the first two tubes in the simulated amplifier. Such drift in the voltages can't be fully accounted for when treating the groups as independent. The drifting, while probably too slow to impact the spectrum of the distorted signal, will modulate various aspects of the distortion (think LFOs).

 

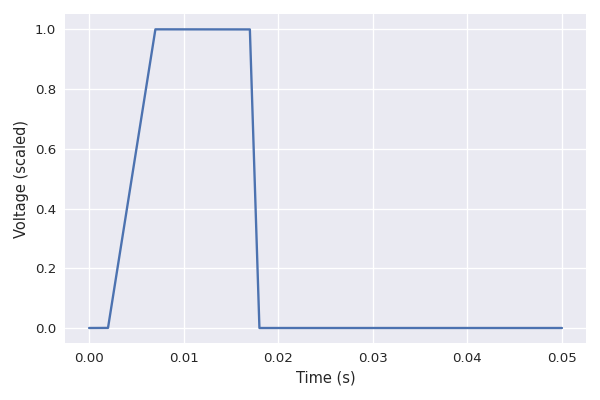
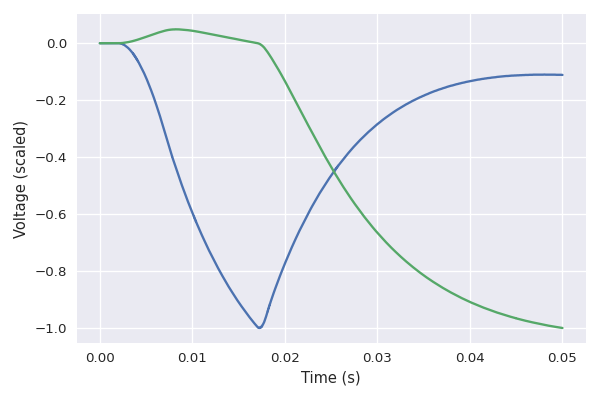
In practical terms: when a note is picked hard, voltages in the amplifier will drift leading to compression, release, and going as far as affecting the tone of what is played next. This leads to effects such as note bloom and sag where the amount of distortion and harmonic richness of the sound are affected by how loud the guitar is being played and has been played in the last few seconds (taken together these effects are often refered to as touch sensitivity).

The approach taken in building Swanky Amp can be summarized as follows: simulate the full amplifier circuit; create algorithms which have the right degrees of freedom to reproduce the observed transformations; and fit the parameters of these algorithms to match the simulation results.

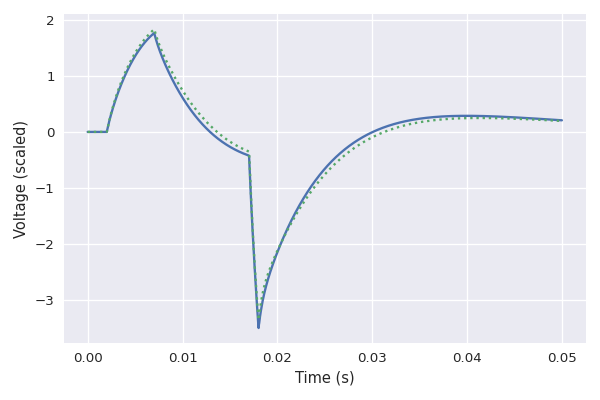
The following image shows the same pulse after it has been transformed by the first pre-amp tube. The blue line is the simulated signal, and the green dotted line is the signal obtained with Swanky Amp's algorithm. In order to correctly fit that shape, the algorithm has taken into account aforementioned voltage drift.

To summarize, Swanky Amp takes tube amplifier modelling a step further: it uses algorithms which capture the interplay of all part of an amplifier's circuit. And this means capturing the breadth of dynamics and touch sensitivity arising from tube amplifiers.